퀵 정렬
- 데이터의 갯수가 적을 때는 괜찮지만 데이터의 갯수가 10만 개만 넘어가도 보통의 상황에서
선택,버블,삽입 정렬 알고리즘을 사용하기가 힘들다. 이런 경우 퀵 정렬을 사용한다면
아무리 많은 양의 데이터라도 빠르게 정렬을 할 수 있다. - 대표적인 분할 정복 알고리즘
- c 라이브러리로 제공하는 sort() 함수가 퀵 정렬을 기반으로 구현되어 있다.
- 이미 정렬이 되어있거나 거의 정렬되어 있는 데이터에 사용할 때는 성능이 매우 떨어짐
퀵 정렬의 시간 복잡도
평균 : O(N * logN) -> 반씩 쪼개서 정렬하기 떄문에 logN인 것이다.
최악 : O(N^2)
퀵 정렬이 최악인 경우에도 O(N * logN)을 보장하는 방법
- STL 라이브러리에서 제공하는 sort() 함수는 퀵 정렬을 기반으로 하되 별도의 처리를 거쳐
최악의 경우에도 O(N * logN)을 보장한다.
퀵 정렬 동작 방식
1. 데이터들 중 특정한 값을 피벗(Pivot)으로 정한다. => 기준값 설정
2. 피벗을 기준으로 왼쪽에는 피벗보다 작은 값들 오른쪽에는 피벗보다 큰 값들이 모이도록 한다.
3. 왼쪽과 오른쪽을 각각 퀵 정렬을 수행한다. => 재귀 호출
4. 최종적으로 전체 값들이 정렬된다.
배열의 중앙을 피벗(Pivot)으로 잡고 하는 법

(1) left, right, pivot 설정

(2) left : pivot보다 큰 값을 찾을 때까지 이동(left++) / right : pivot보다 작은 값을 찾을 때까지 이동(right--)

- pivot보다 큰 값(left)과 작은 값(right)을 찾고, 서로의 값을 교환
- 교환한 후 left++ , right--
(3) 위와 같은 과정을 반복해서 피봇보다 큰 값(left)과 작은 값(right) 찾아서 교환

- 교환한 후 left++, right--;
(4) 값을 교환한 후 left와 right가 엇갈림 ( ☆☆☆☆☆ )
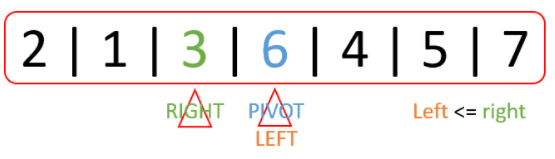
- left와 right가 엇갈려 left가 더 커지게 된 경우
=> right와 left 두 부분으로 분할해서 따로 퀵 정렬 수행!!
(5) 분할된 두 부분을 각각 퀵 정렬 수행 ( 재귀 호출 )

퀵 정렬 구현 코드
#include<iostream>
using namespace std;
int data[] = {5,1,6,3,4,2,7};
void quickSort(int start, int end){
if(start >= end) return;
int left = start;
int right = end;
int pivot = (start + end) / 2;
while(left < right){
while(data[left] < data[pivot]) left++;
while(data[right] > data[pivot]) right--;
if(left <= right){
swap(data[left], data[right]);
left++;
right--;
}
}
quickSort(start,right);
quickSort(left,end);
}
int main(){
int i;
quickSort(0,6);
for(i = 0; i < 7; i++){
printf("%d ",data[i]);
}
}'알고리즘 개념' 카테고리의 다른 글
| 힙 정렬 ( Heap sort ) (0) | 2022.02.11 |
|---|---|
| C++ STL sort() 함수 다루기 (0) | 2022.02.10 |
| 병합 정렬 ( Merge sort ) (0) | 2022.02.09 |
| 버블 정렬 ( Bubble sort ) (0) | 2022.02.09 |
| 삽입 정렬(insertion sort) (0) | 2022.02.08 |
